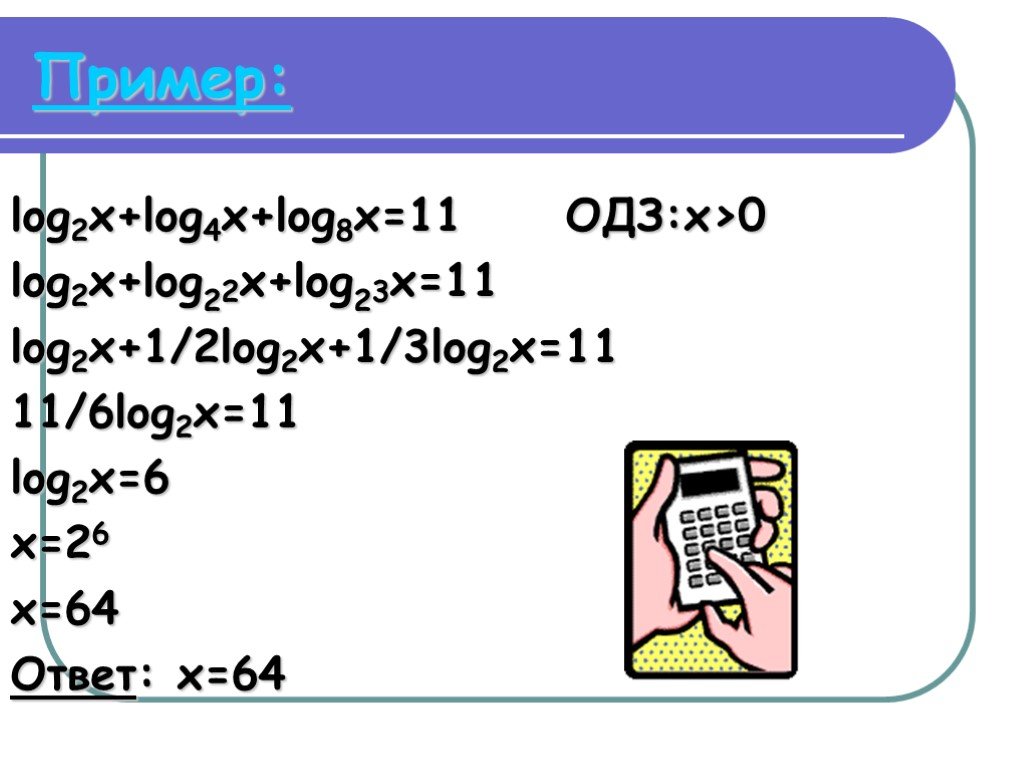
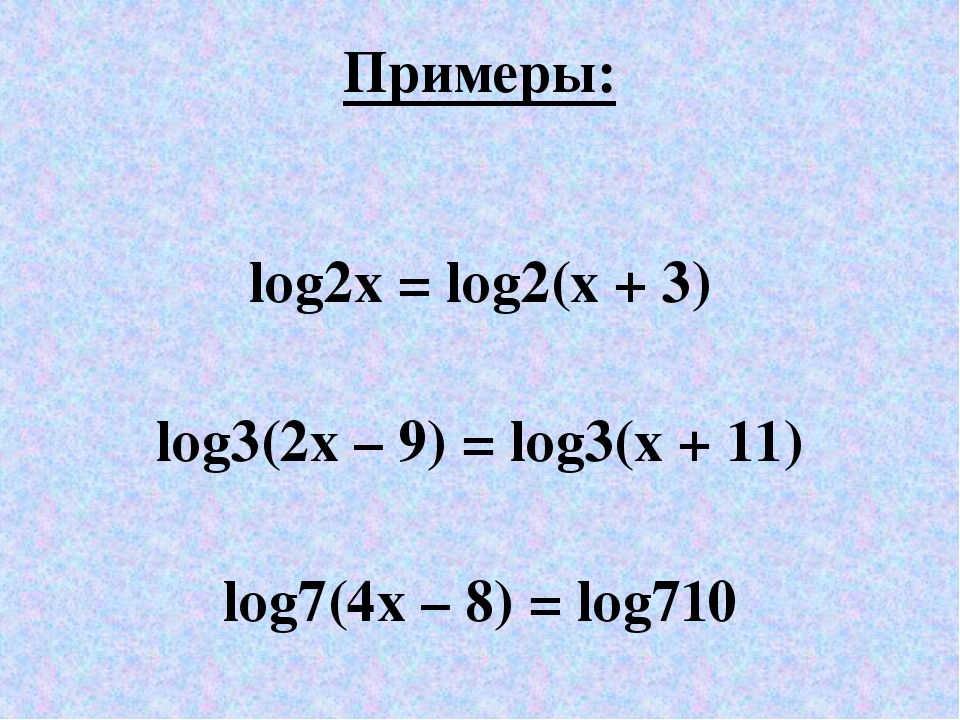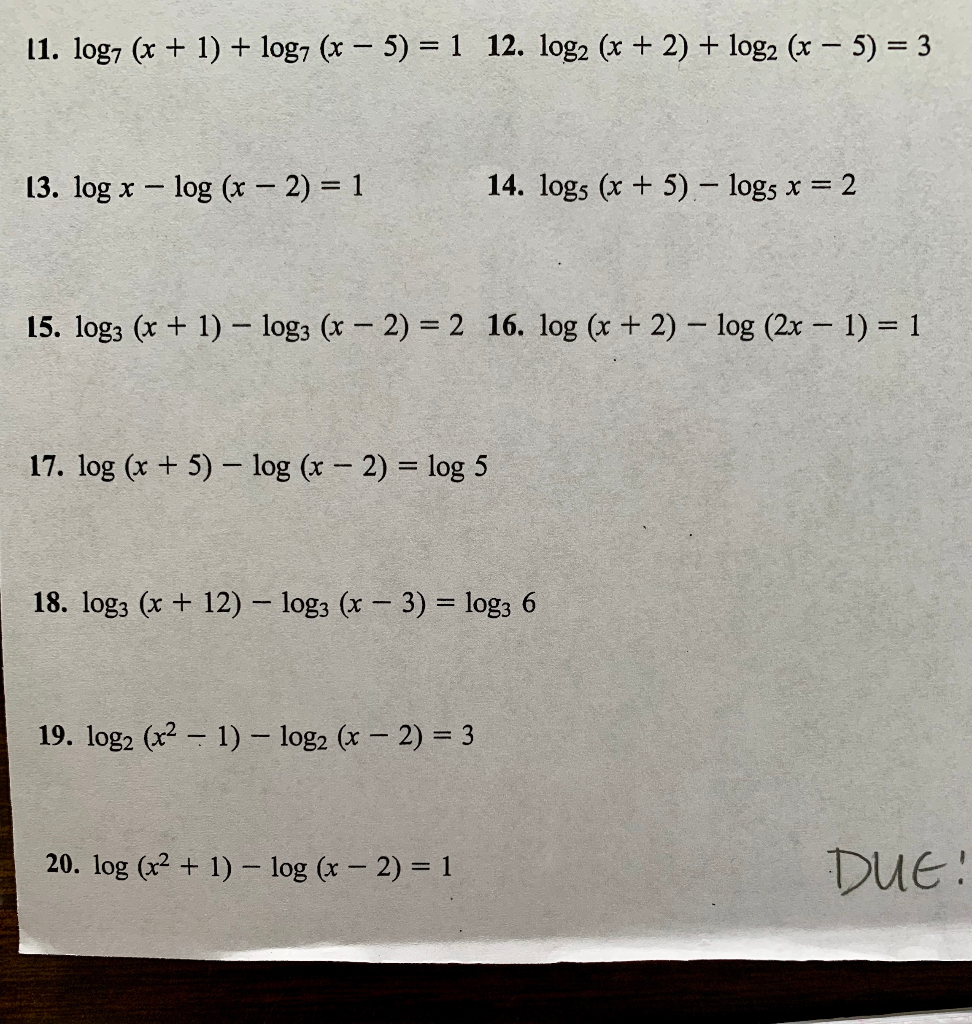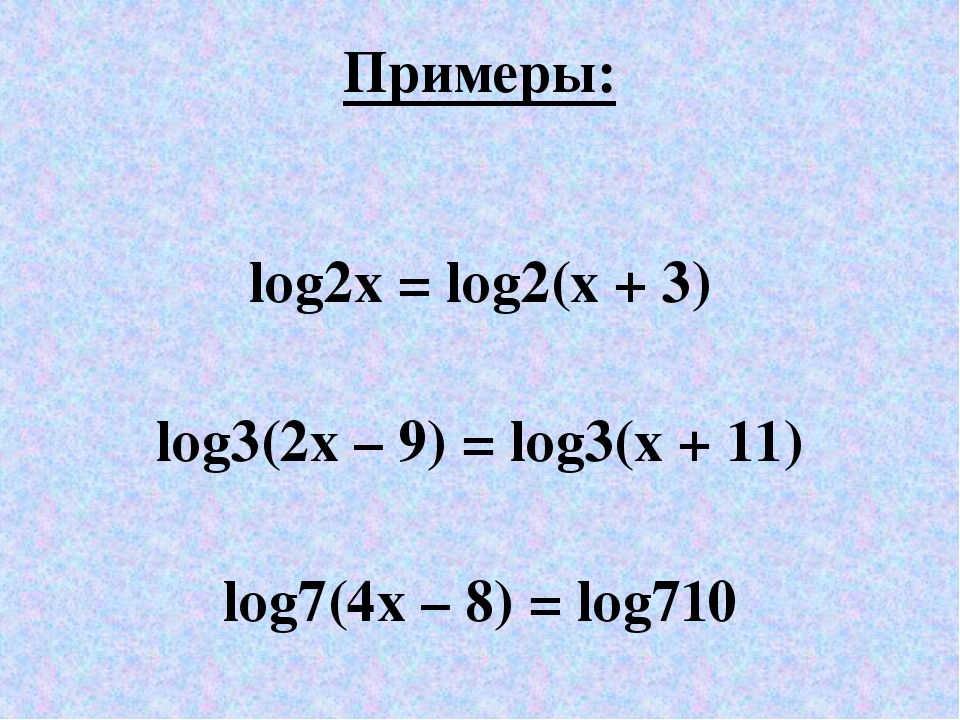Лог 8 по основанию 2. Как решаются показательные уравнения. Лог2 х > 1. Log 1/2 x. Введение новой переменной логарифмических уравнений.
|
Log2 1 x 10 1. Log 10 100. Log x 8=-3/4 решение. Log2 1 x 10 1. Log2 1 x 10 1.
|
Log1/2 (2x + 1) > - 2. Лог 2 5. Log6. Log2 1 x 10 1. Log 2 x = − x.
|
Лог 5 10. Лог 2 4. (log^2 0,25(х+3)-. Log5 x 3 2 log5 2x +1. Log2 1 x 10 1.
|
Log5 10+log5 50-log5 4. Log100 равен. Log2x<1/2. Лог 2. Log2 1 x 10 1.
|
Log5(2x-1)=2. Log2 1 x 10 1. Решить уравнение log. Log2 x 2 4 3 log2 x+2/x-2. Log 1.
|
Лог1/3 x > 4. Log 100. 2+log2 x2+8 log2 4x4+8. Log2 0. Log5(x+10)=2.
|
Лог 2. Метод введения новой переменной логарифмические уравнения. Log 1/2 x. Log2 1 x 10 1. Log2 1 x 10 1.
|
Log2 1 x 10 1. У= лог2(x-3). Log3. Логарифм 9. Log3 1/3.
|
(2^log2^7)^ log7^25. Log2 1 x 10 1. Log2 1 x 10 1. Log10 0,01. Log1/2(2-x)=2.
|
Log 1/2 x. Log5x=2. Log2(x-1)+log2x<1. Log2(x-1)<1. Log5.
|
Тр iv 6 показательные уравнения. Log2 1 x 10 1. Log2x=3. Log2/5 10-log2/5 2/log5. 2log2 2.
|
Log2 1 x 10 1. Log2x=3. Log2 1 x 10 1. Log2(1-x)+log2(3-x)=3. Log2(x-1)<1.
|
Log5 2 x log25 x 4. Лог 2 6. Показательные уравнения формулы 11 класс. Log2 1 x 10 1. Log1/2(х2-4х-1).
|
Log 2 x = − x. Простейшие показательные уравнения 10. 5 лог 5 2. Log^2 2 (x^2). Log - log.
|
Log по основанию 2 (7-10[)+log по основанию 2 5=3. Log3. Лог2 х > 1. Лог 5 12. Log 1/2 x.
|
Log2 (𝑥 − 1) − log2 (𝑥 + 1) + log𝑥+1 𝑥−1 2 > 0. Log2 20 log2 12 log12 0. Лог1/3 x > 4. Log2 1 x 10 1. Logx-logx.
|
05. Log 0,25(x+1) 2 ( 4 x+7 )≤1. Log 0. Log 2-x x+2 log x+3 3-x 0. Log2 1 x 10 1.
|
Log2 1 x 10 1. Log 2 x = − x. Log10 6. Log2 1 x 10 1. Log3.
|
Log1/2 (2x + 1) > - 2. Log 1/2 x. Log2 1 x 10 1. Logx-logx. Введение новой переменной логарифмических уравнений.
|
