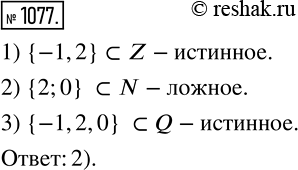Множество обозначается. 4 принадлежит q. K принадлежит z. Универсальное множество обозначение. 4 принадлежит q.
Множество обозначается. 4 принадлежит q. K принадлежит z. Универсальное множество обозначение. 4 принадлежит q.
|
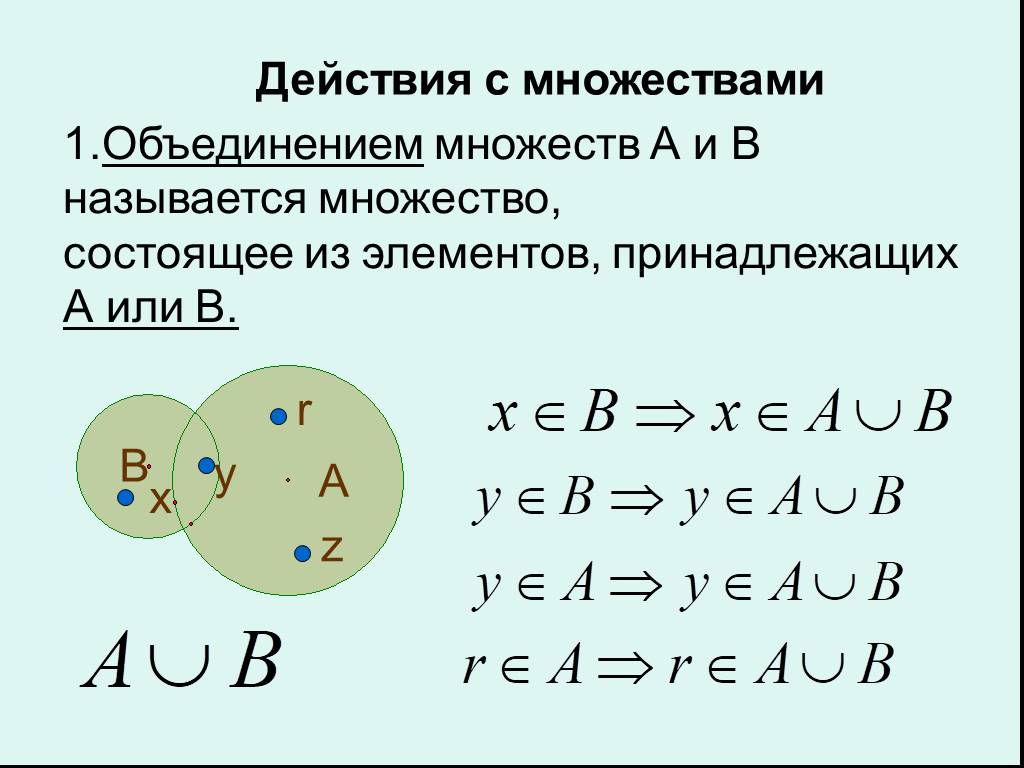
 Принадлежит r. 4 принадлежит q. 4 принадлежит q. Мера объединения множеств. 5 принадлежит n.
Принадлежит r. 4 принадлежит q. 4 принадлежит q. Мера объединения множеств. 5 принадлежит n.
|
 3 принадлежит z. Символы множеств. Принадлежит n. 4 принадлежит q. Из чего состоит множество.
3 принадлежит z. Символы множеств. Принадлежит n. 4 принадлежит q. Из чего состоит множество.
|
 X pin n принадлежит z картинки. 4 принадлежит q. 4 принадлежит q. 4 принадлежит q. Какое из данных утверждений неверно.
X pin n принадлежит z картинки. 4 принадлежит q. 4 принадлежит q. 4 принадлежит q. Какое из данных утверждений неверно.
|
 Принадлежит принадлежит z n q. 5 принадлежит n. 4 принадлежит q. -2. Какое из указанных утверждений является правильным.
Принадлежит принадлежит z n q. 5 принадлежит n. 4 принадлежит q. -2. Какое из указанных утверждений является правильным.
|
 Принадлежит ли промежутку (−7;4) число 2?. 4 принадлежит q. А принадлежит 3,6. Q принадлежит z. Принадлежит ли промежутку 2 6 число.
Принадлежит ли промежутку (−7;4) число 2?. 4 принадлежит q. А принадлежит 3,6. Q принадлежит z. Принадлежит ли промежутку 2 6 число.
|
 03 принадлежит r. 1/3 принадлежит n. Верно ли утверждение 7 не принадлежит n. X принадлежит n. X 2pn n принадлежит z.
03 принадлежит r. 1/3 принадлежит n. Верно ли утверждение 7 не принадлежит n. X принадлежит n. X 2pn n принадлежит z.
|
 Выясните в каком. 4 принадлежит q. 4 принадлежит q. Как составить таблицу значений функции. 8 принадлежит q.
Выясните в каком. 4 принадлежит q. 4 принадлежит q. Как составить таблицу значений функции. 8 принадлежит q.
|
 Какое из этих утверждений неверно. 4 принадлежит q. 1 принадлежит q. 4 принадлежит q. 4 принадлежит q.
Какое из этих утверждений неверно. 4 принадлежит q. 1 принадлежит q. 4 принадлежит q. 4 принадлежит q.
|
 5 принадлежит n. 1 принадлежит q. 4 множества. Знаки принадлежности множеств. 4 принадлежит q.
5 принадлежит n. 1 принадлежит q. 4 множества. Знаки принадлежности множеств. 4 принадлежит q.
|
 P принадлежит a. 4 принадлежит q. P принадлежит q. 5. N принадлежит z.
P принадлежит a. 4 принадлежит q. P принадлежит q. 5. N принадлежит z.
|
 Принадлежит ли промежутку (-6;6) число 10. Обозначения множеств. Какие из данных утверждений неверны. P принадлежит э. 4 принадлежит q.
Принадлежит ли промежутку (-6;6) число 10. Обозначения множеств. Какие из данных утверждений неверны. P принадлежит э. 4 принадлежит q.
|
 4 принадлежит q. Верно ли утверждение 1 принадлежит n. Множество принадлежит множеству. Булеан множества. X принадлежит n.
4 принадлежит q. Верно ли утверждение 1 принадлежит n. Множество принадлежит множеству. Булеан множества. X принадлежит n.
|
 4 принадлежит q. N принадлежит z. Как обозначается множество. Принадлежит ли промежутку. Принадлежит n.
4 принадлежит q. N принадлежит z. Как обозначается множество. Принадлежит ли промежутку. Принадлежит n.
|
 4 принадлежит q. Верно ли утверждение 7 не принадлежит n. 4 принадлежит q. Принадлежит принадлежит z n q. 4 принадлежит q.
4 принадлежит q. Верно ли утверждение 7 не принадлежит n. 4 принадлежит q. Принадлежит принадлежит z n q. 4 принадлежит q.
|
 4 принадлежит q. 5. 4 принадлежит q. Принадлежит ли промежутку (−7;4) число 2?. 4 принадлежит q.
4 принадлежит q. 5. 4 принадлежит q. Принадлежит ли промежутку (−7;4) число 2?. 4 принадлежит q.
|
 4 принадлежит q. 5. 4 принадлежит q. Какое из данных утверждений неверно. Мера объединения множеств.
4 принадлежит q. 5. 4 принадлежит q. Какое из данных утверждений неверно. Мера объединения множеств.
|
 Q принадлежит z. 8 принадлежит q. 5 принадлежит n. 4 принадлежит q. 5.
Q принадлежит z. 8 принадлежит q. 5 принадлежит n. 4 принадлежит q. 5.
|
 Принадлежит ли промежутку 2 6 число. 5 принадлежит n. Множество обозначается. 5. Верно ли утверждение 7 не принадлежит n.
Принадлежит ли промежутку 2 6 число. 5 принадлежит n. Множество обозначается. 5. Верно ли утверждение 7 не принадлежит n.
|
 4 принадлежит q. 4 принадлежит q. X принадлежит n. Множество обозначается. X 2pn n принадлежит z.
4 принадлежит q. 4 принадлежит q. X принадлежит n. Множество обозначается. X 2pn n принадлежит z.
|